Counting solutions to equations

2019-Apr-8

There are \(\binom{n-1}{m-1}\) integer compositions of \(n\) with \(m\) parts. Complex polynomials of degree \(n\) have \(n\) zeros, counting multiplicity. Where else do we count solutions to equations? Our criteria are that the equations must be parametrized, and that for each parameter value there is a finite solution set. Some examples are given.

Integer solutions in a ball:

Theorem: If \(f\) is a polynomial over \(\mathbb{Z}\) in \(n\) variables, let

\[N(f, B) = |\{\mathbf{x} \in \mathbb{Z}^n: f(x_1, \ldots, x_n) = 0, \max_i |x_i| \leq B \}|.\]

If \(f\) is a singular homogeneous polynomial over \(\mathbb{Z}\) of degree \(d\) in \(n > (d-1)2^d\) variables, then \(N(f, B) \sim c_f B^{n-d}, B \to \infty\), under some technical conditions.

Diophantine equations:

Theorem: Say \(f\) is a polynomial of degree \(d\) over \(\mathbb{Z}_p\) where \(GCD(p,d) = 1\). If \(N(f)\) is the number of solutions \(\mathbf{x} \in \mathbb{Z}_p^n\) to \(f(\mathbf{x}) = 0\), then \(N(f) = p^{n-1} + O(p^{n/2}), p \to \infty\), assuming a non-singularity condition.

Non-negative integer solutions to linear equations:

E.g. \(\{ (x,y,z) : 3x + 5y + 17z \leq \lambda, x \geq 0, y \geq 0, z \geq 0 \}\).

Theorem: Let \(\Delta(\lambda) = \{ \mathbf{x} \in \mathbb{Z}^n: M \mathbf{x} \leq \lambda\mathbf{b} \}\). Then \(|\Delta(\lambda)|\) is a polynomial in \(\lambda\) of degree \(n\).

Note that wlog \(\mathbf{b}\) takes possible values \(-1,0,1\). If not, multiply \(b_i\) and \([M]_{i,*}\) by \(\textrm{lcm}(\mathbf{b})/b_i\) and set \(\lambda' = \lambda / \textrm{lcm}(\mathbf{b})\).

If \(\mathbf{b}\) takes possible values \(-1,0,1\), we may take the difference \(\Delta(\lambda) \setminus \Delta(\lambda -1)\) to get solutions to an equality.

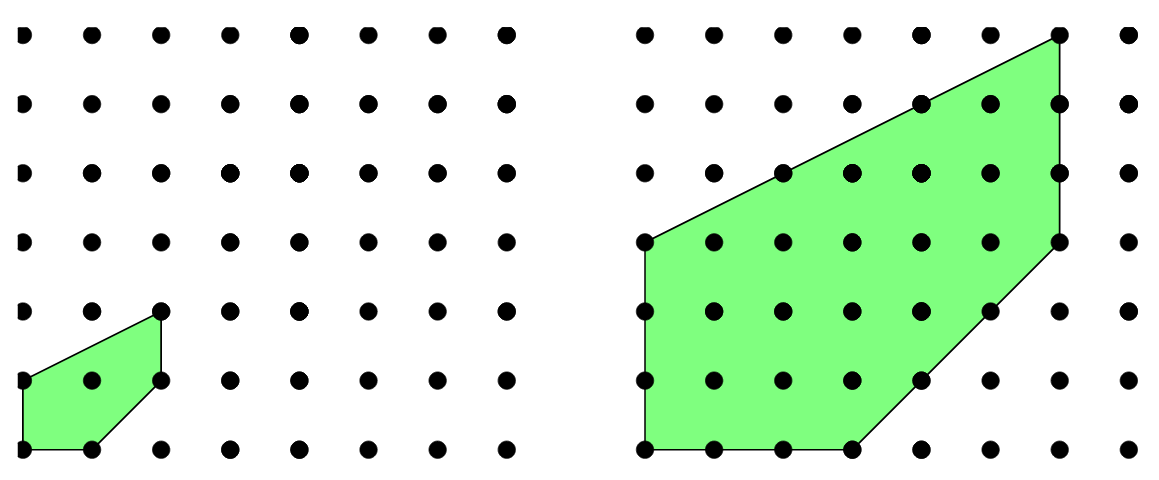(Above: Example solution sets for different values of \(\lambda\).)

Locally restricted words over finite groups:

Theorem: If \(G\) is a finite group and \(x_1, \ldots, x_m \in G\), let \(N(m, a)\) be the number of solutions to \(x_1 \cdots x_m = a\) such that \((x_1, \ldots, x_m)\) satisfies a local restriction. Then under some conditions, as \(m \to \infty\) we have \(N(m, a) \sim N(m, e)\), where \(e \in G\) is the identity element.